The fatigue phenomenon
Mechanical fatigue is a phenomenon that occurs when a mechanical component is repeatedly stressed with variable or repeated loading. Each time the load is applied, the material is damaged (local alteration of the material). Thus, the maximum permissible fatigue load is lower than the maximum permissible static load.

Performing an fatigue resistance analysis, what are the stakes?
Numerical simulation makes it possible to evaluate the stress levels and deformations of a mechanical part right from the design phase. It is important to consider the fatigue phenomenon to ensure the durability and reliability of components subjected to variable and repeated loading over time to know the service life before crack initiation, and then the remaining service life associated with crack propagation. All industrial sectors (automotive, aeronautics, naval, railway, watchmaking, etc.) are concerned by fatigue issues. Indeed, a car suspension wishbone, a landing gear or a special machine manufactured in large series undergoes a large number of loads during their lifespan.
The main steps in a fatigue analysis are as follows:
- Loading cycle characterisation
- Finite element modelling of the behaviour of the structure
- Definition of fatigue criteria (uniaxial or mutliaxial)
- Definition of material fatigue behaviour (SN curves),
- Average constraint effect integration (Haig diagram)
- Damage calculation
- Lifespan evaluation
Fatigue under quasi-static or dynamic loads
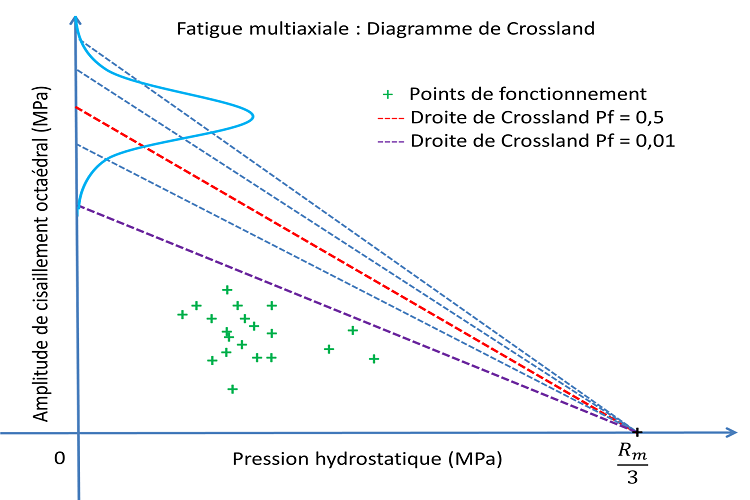
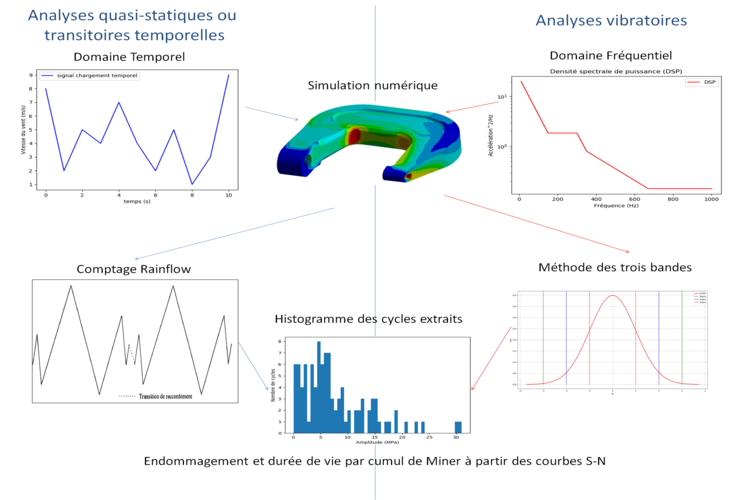
The lifespan of components or systems subjected to repeated static loading or time signals can be evaluated based on static or crash simulations (user-defined cycles), and time transitory simulations that allow the evolution of stress levels to be known and the different fatigue cycles to be identified (Rainflow counting). Each cycle is the cause of damage calculated from the Wöhler curve of the material. The total damage is then calculated by linear Miner accumulation. Uncertainties in the input parameters of the model (thickness, material characteristics) can be considered in order to evaluate the lifespan for a probability of occurrence. Multi-axial stress states can also be handled by using one of the following fatigue criteria.
- Crossland
- Dang Van
Vibratory fatigue
The vibration fatigue lifespan of systems subjected to all types of dynamic loading (sinus, random…) can be evaluated. The approach used is based on statistical cycle distribution methodologies such as Steinberg, Lalanne, Dirlik and on material characteristic curves (Wölher). Uncertainties in the input parameters of the model can also be considered in the calculation chain to estimate a probability density of the damage.
Fissure propagation
The study of fissure propagation and the estimation of the lifespan after fissure initiation is also part of the suggested fatigue analyses. The Paris law is the most widely used method to know the evolution of the fissure depth associated with each new loading cycle applied. It is based on the calculation of the stress intensity factor at the fissure tip obtained from the shape of the defect (semi-elliptical for example) and the stresses measured.
