Contexte
Aubert & Duval, spécialiste de la métallurgie haut de gamme, est un leader mondial dans la conception, le développement et la fabrication de pièces forgées, matricées, de barres ou de poudres en aciers hautes performances, en superalliages, en aluminium ou en titane.
Afin de maîtriser et optimiser les microstructures sur produits, Aubert et Duval réalise des essais de laboratoire sur éprouvettes et développe des modèles ayant pour objectif de prédire l’évolution microstructurale (fraction recristallisée et la taille des grains recristallisés) sous les effets de la température et de la déformation.
Ces modèles phénoménologiques utilisent en entrées des informations sur la structure initiale, des données thermomécaniques, ainsi que des constantes identifiées par méthode inverse grâce à un solveur.
Aubert & Duval a constaté une certaine dispersion entre les sorties de leurs modèles de recristallisation et leurs mesures issues d’essais de torsion et compression. Aubert & Duval a donc fait appel aux compétences de Phimeca pour les accompagner dans leur démarche d’enrichissement / amélioration de leurs modèles de recristallisation.
Objectifs
- Fournir à Aubert & Duval des outils pour mieux visualiser le comportement des données à leur disposition ;
- Améliorer leur modèle de recristallisation en testant d’autres méthodes pour optimiser les constantes des modèles phénoménologiques ;
- Construire un modèle de Machine Learning permettant de prédire la fraction recristallisée et la taille de grains recristallisés, afin de voir l’apport que peut avoir une approche uniquement basée sur la donnée.
Réalisations
- Analyse descriptive des données à disposition à l’aide de notebooks python et de l’outils Persalys :
- Histogrammes ;
- Boxplots ;
- Matrice de corrélation ;
- Diagramme en coordonnées parallèles permettant d’établir des liens entre les valeurs prises par les différentes variables ;
- …
- Implémentation en Python des modèles phénoménologiques fournis par Aubert & Duval.
- Utilisation de différentes approches pour optimiser les constantes du modèle phénoménologique de la fraction recristallisé :
- Méthodes d’optimisation par descente de gradient, avec et sans contraintes ;
- Algorithmes d’évolution différentielle (inspirés par les algorithmes génétiques et les stratégies évolutionnistes).
- Construction de modèles de Machine Learning permettant de prédire la fraction recristallisée et la taille de grains recristallisés. Extraction de l’importance prise par les variables dans la prédiction du modèle.
- Mise à disposition de l’outil Persalys et de notebooks interactifs synthétisant les résultats de l’étude et permettant au client d’explorer ses données par lui-même.
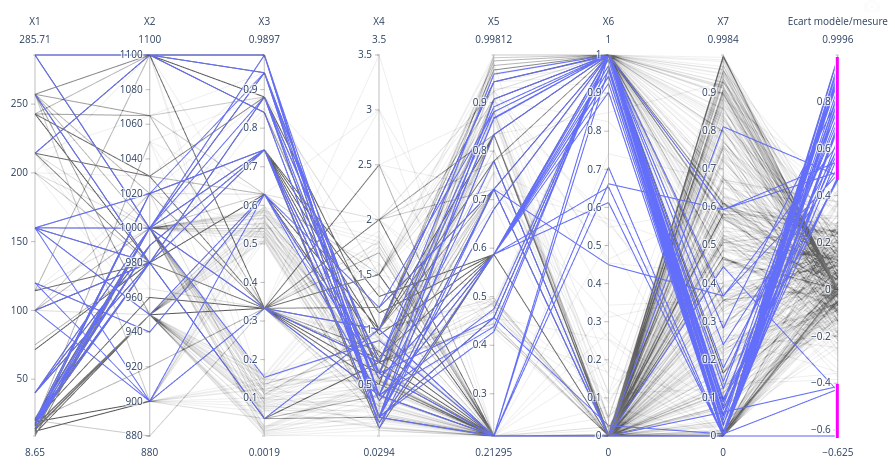
Figure 1 : Graphique de coordonnées parallèles permettant d’identifier les liens entre les variables d’entrées et les écarts entre le modèle et les mesures
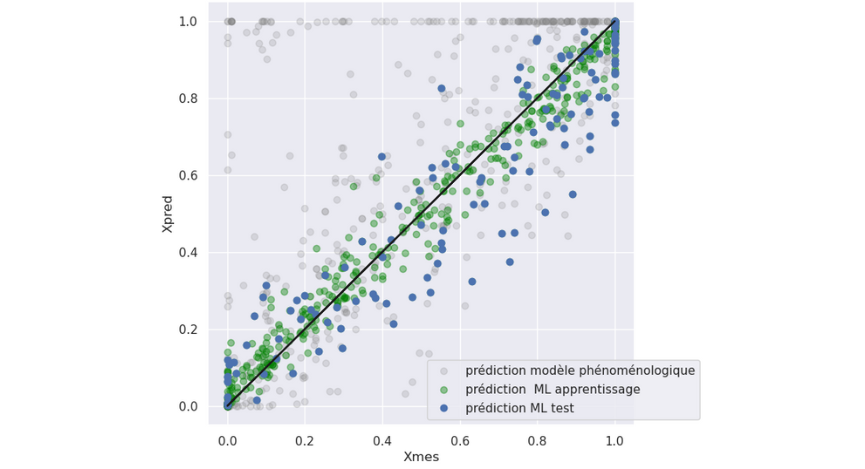
Figure 2 : Graphique d’adéquation entre les mesures et les prédictions des modèles phénoménologique et Machine Learning
